Gamma distribution explains several life events such as mechanical machines and tools reliability, predicted rainfall, or any applications with positive results. However, these applications are usually unbalanced. Hence the reason behind the distribution’s skewed shape.
Further, it is among the distributions used widely in Engineering, science, and business. Thus, it is used to model the continuous variable that should have a skewed and positive distribution.
Again, the Gamma distribution is a type of statistical distribution that’s associated with the beta distribution. In this article, we’ll explore the Gamma distribution parameters, their properties, mean, variance, formula, examples, etc.
Table of Contents
Meaning of Gamma Distribution
The gamma distribution is a distribution with two parameters (inverse scale and shape parameter) with continuous probability distributions.
It is associated with the exponential distribution, Erlang distribution, normal distribution, and chi-squared distribution. The Gamma function is denoted by ‘Γ’.
Additionally, they have two free parameters—Alpha (α) and Beta (β). Where:
α = Shape parameter
β = Rate parameter (the reciprocal of the scale parameter)
It is characterized by mean µ=αβ and variance σ2=αβ2
The scale parameter β is only used to scale the distribution. You can understand this by remarking that anywhere the random variable x appears in the probability density. Afterward, it is divided by β.
Since the scale parameter gives you the dimensional data, it is often useful to work with the “standard” gamma distribution, that is, with β = 1.
What Are The Properties of Gamma Distribution?
We can spot the following properties from the Gamma distribution’s shape:
- The value of the Gamma distribution is the factorial of (n-1) for real numbers (n).
- The square root of pi is the value of the Gamma distribution of 1/2.
- It advances to zero as time tends to infinity.
Mathematically, the properties of gamma distribution are as follows:
For any positive (+ve) real number α,
Γ(α) = 0∫∞ ( ya-1e-y dy), for α > 0.
0∫∞ ya-1 eλy dy = Γ(α)/λa, for λ >0.
Γ(α +1)=α Γ(α)
Γ(m)=(m-1)!, for m = 1,2,3 …;
Γ(½) = √π
Gamma Distribution Parameters
The shape and scale parameters are the two main factors we use to characterize the Gamma distribution. For a more precise description, we can use the shape, scale, and threshold parameters in statistics to characterize the distribution.
This implies that we must set the threshold parameter to zero to employ the two-parameter system.
A probability density function, or PDF, is a formula that contains the factors that determine the distribution’s attributes and is used to define the Gamma distribution. For instance, the Gamma distribution’s PDF looks like this:
As you can see, the distribution depends on the denominator’s Gamma function and the numerator’s shape and scale parameters. The Gamma function is defined for positive integers and complex numbers, and it extends the factorial function to complex numbers.
1. The Shape Parameter
The shape distribution (alpha) is the first of the two primary parameters of the Gamma distribution. Further, the number of occurrences that the distribution describes is indicated by the shape parameter. For instance, the shape distribution will be four if we model four accidents and use the Gamma distribution to explain the probability of car accidents in a specific city.
Meanwhile, the number of events, or the shape distribution, must be positive but need not be an integer.
2. The Scale Parameter
The scale parameter (beta) is the second major parameter. It explains the period between the events we are modeling. If we were to repeat the example of the vehicle accidents, we would take the average amount of time between the four accidents to determine the duration between them.
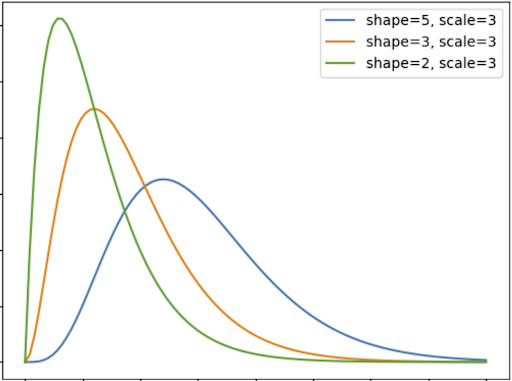
So, the peak height of the distribution is determined by the scale parameter. The higher the scale distribution’s value, it will be spread, which implies it will have a lower peak. On the other hand, the distribution will narrow and the peak will enlarge if the scale parameter is small.
3. The Threshold Parameter
This parameter determines whether the distribution allows negative values. Usually set to zero, this option indicates that only positive values can be accepted by the distribution. This is because most applications where the Gamma distribution is used do not allow for negative values.
So, let’s say that the other two parameters remain unchanged. When such happens, the threshold parameter displays the distribution values for negative values.
However, you may remember that we previously stated that the Gamma is limited to positive values. Therefore, for negative values, the Gamma distribution has a value of zero.
Gamma Function
Γ(y) represents the Gamma function. It is an extended form of factorial function to complex real numbers. Thus, if n∈{1,2,3,…}, then Γ(y)=(n-1)!
If Alpha (α) is a positive real number, we define Γ(α) as:
Γ(α) = 0∫∞ ( ya-1e-y dy), for α > 0.
If α = 1, Γ(1) =0∫∞ (e-y dy) = 1
If the variable is changed to y = λz, then we can use this definition for gamma distribution: Γ(α) = 0∫∞ ya-1 eλy dy where α, λ >0.
Gamma Distribution Formula
The Gamma distribution formula is as follows:
Where;
P and x are continuous random variables.
Gamma Distribution Mean
You can determine the Gamma distribution in two ways:
- Directly.
- Broadening the moment generation function.
It is also regarded as the expected value of the distribution.
Gamma Distribution Variance
It is represented as follows:
So, Variance = E[x2] – [E(x2)], where;
p = (E(x)) (Mean and Variance p(p+1) – p2 = p
Read this article: How to Calculate a Statistics Critical Value
Uses of Gamma Distribution
This distribution can be used in the following ways:
1. Time Modeling
A gamma distribution can be used to model wait times. For example, how long do you have to wait for the next train or bus to arrive assuming they have a flexible schedule? Again, you can use this distribution to calculate the probability that two trains will arrive at the same time.
2. Queuing Theory
We’ve all at some point queued up for food before. How long will it take the barista to make your latte? What the Queuing Theory does is simulate a queue of clients that need a service by considering certain parameters like the number of staff at a particular time, the rate of service, the rate of individuals joining the line vs those leaving it, the place of service’s capacity, etc.
3. Reliability Modeling
Again, you can use the Gamma distribution to calculate how long a product will last and to measure the dependability of a specific piece of technology. Thus, how many hours can a gadget function before its performance degrades? That computer you recently acquired can operate seamlessly for about 9,000 hours on average. So, what’s the probability of the laptop running properly for 6 to 12 months? What about 12 to 18 months? You can use this distribution to answer these questions.
Conclusion
The Gamma distribution is a continuous probability distribution commonly used to model events like waiting times, failures, and intervals with an inherent positive skew.
Defined by two parameters, this distribution is flexible enough to model data from various domains.
Its key properties like being skewed to the right and only defined for positive values make it useful for situations involving durations, levels, or concentrations.