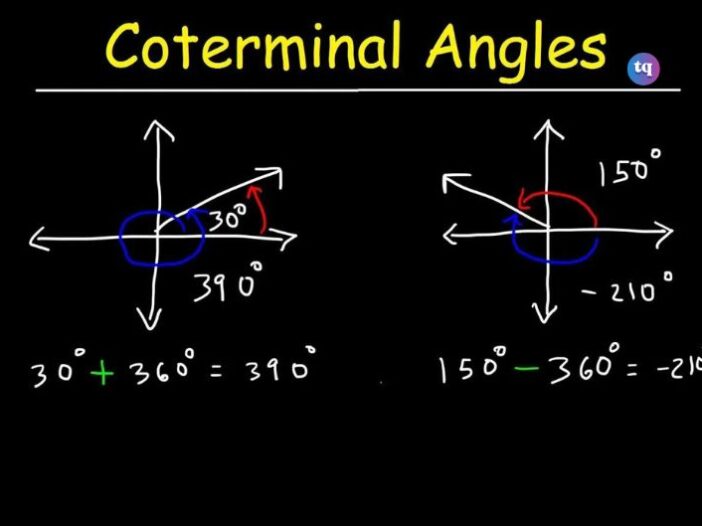
Coterminal angles are angles that have the same initial and terminal sides but differ by a multiple of 360 degrees (or 2π radians). To find coterminal angles in radians, you can follow these steps:
Identify the given angle in radians.
Add or subtract a multiple of 2π radians until you obtain an angle that has the same initial and terminal sides as the given angle.
Repeat step 2 as necessary to find all coterminal angle.
For example, suppose you are asked to find coterminal angles in radians for an angle of θ = 7π/4. Here’s how you can do it:
- The given angle is θ = 7π/4.
To find a positive coterminal angle, add 2π radians to θ:
θ + 2π = 7π/4 + 2π = 15π/4
To find a negative coterminal angle, subtract 2π radians from θ:
- θ – 2π = 7π/4 – 2π = -π/4
To find additional coterminal angles, add or subtract 2π from the previously obtained angles as necessary. For example:
15π/4 + 2π = 23π/4
- -π/4 – 2π = -9π/4
So, the coterminal angles in radians for θ = 7π/4 are:
7π/4, 15π/4, -π/4, -9π/4.
Note that there are infinitely many coterminal angles for any given angle, but the above steps can help you identify a few of them.
Table of Contents
Identify the Given Angle in Radians:
To identify a given angle in radians, you need to know the measure of the angle in terms of radians. Radians are a unit of angle measurement used in mathematics and physics, where one radian is equal to the angle subtended at the centre of a circle by an arc equal in length to the radius of the circle.
Angles in radians are denoted by the symbol “θ” and are measured in terms of π (pi) which is an irrational number approximately equal to 3.14159. A complete circle is equal to 2π radians, while a straight angle is equal to π radians.
For example, if you are given an angle of 45 degrees, you can convert it to radians by multiplying by π/180 since there are π/180 radians in one degree. Therefore, 45 degrees is equal to (45π/180) = π/4 radians.
Alternatively, if you are given an angle in terms of a fraction of a circle, you can convert it to radians by multiplying by 2π. For example, if you are given an angle of 1/3 of a circle, you can convert it to radians by multiplying 2π by 1/3 to get (2π/3) radians.
In summary, to identify a given angle in radians, you need to know the measure of the angle in terms of π. If the angle is given in degrees, you need to convert it to radians using the conversion factor π/180. If the angle is given as a fraction of a circle, you need to multiply the fraction by 2π to convert it to radians.
See Also: How to Fix Disney Plus Error Code 39
Least Positive Coterminal Angle:
The least positive coterminal angle is the angle that has the same initial and terminal sides as the given angle, but is positive and the smallest possible angle that satisfies this condition.
To find the least positive coterminal angle of an angle in degrees or radians, you can follow these steps:
- Convert the angle to radians if it is given in degrees. To do this, multiply the degree measure by π/180.
- Divide the angle by 2π to find how many full circles the angle makes. The remainder gives the fractional part of a circle that the angle covers.
- Multiply the fractional part of the circle by 2π to find the angle in radians that is less than a full circle.
- If the resulting angle is negative, add 2π radians to make it positive.
- The resulting angle is the least positive coterminal angle.
For example, suppose you are given an angle of 540 degrees. The steps to find the least positive coterminal angle are:
- Convert the angle to radians: 540 degrees * π/180 = 3π radians.
- Divide by 2π: 3π / 2π = 1 and a half circles. The remainder is π/2.
- Multiply by 2π: π/2 * 2π = π.
- Since the resulting angle is positive, no adjustment is necessary.
- The least positive coterminal angle is π radians.
Therefore, the least positive coterminal angle of 540 degrees is π radians.
Conclusion:
In conclusion, finding coterminal angles in radians involves adding or subtracting 2π (or any multiple of 2π) to an angle until you obtain an angle between 0 and 2π. This allows for the identification of coterminal angles, which share the same initial and terminal sides but differ by a multiple of 2π.
FAQs on Coterminal Angles in Radians
A given angle has infinitely many coterminal angles, so you cannot list all of them. You can write them down with the help of a formula. If your angle θ is expressed in degrees, then the coterminal angles are of the form θ + 360°×k, where k is an integer (maybe a negative number!). If θ is in radians, then the formula reads θ + 2π×k.
Two angles, α and β, are coterminal if their difference is a multiple of 360°. That is, if β - α = 360°×k for some integer k. For instance, the angles -170° and 550° are coterminal, because 550° - (-170°) = 720° = 360° × 2. If your angles are expressed in radians instead of degrees, then you look for multiples of 2π, i.e., the formula is β - α = 2π×k for some integer k.
The coterminal angles of 45° are of the form 45° + 360°×k, where k is an integer. Plugging in different values of k, we obtain different coterminal angles of 45°. Let us list several of them:45°, 405°, 765°, -315°, -675°.
Coterminal angles are those angles that share the terminal side of an angle occupying the standard position. The standard position means that one side of the angle is fixed along the positive x-axis, and the vertex is located at the origin.
The answer is 280°. To arrive at this result, recall the formula for coterminal angles of 1000°:
1000° + 360°×k. Clearly, to get a coterminal angle between 0° and 360°, we need to use negative values of k. For k=-1, we get 640°, which is too much. So let’s try k=-2: we get 280°, which is between 0° and 360°, so we’ve got our answer.
Leave a Reply